德雪紅¹，張博文¹，金敏¹，吳桂芳¹，翟曉敏²，郭文斌¹

（1.內(nèi)蒙古農(nóng)業(yè)大學(xué)機(jī)電工程學(xué)院，呼和浩特010020；2.航天科工集團(tuán)第六研究所，呼和浩特010076）

　　摘要：精確地表達(dá)生物質(zhì)成型顆粒圓周表面粗糙形貌是生物質(zhì)成型機(jī)關(guān)鍵部件摩擦磨損機(jī)理分析及磨損預(yù)測(cè)研究的關(guān)鍵。選擇原料為混合木屑的生物質(zhì)成型顆粒，在直徑6mm、顆粒度1~3mm、含水率11%、密度1.2g/cm³的條件下，測(cè)出其圓周表面形貌及輪廓數(shù)據(jù)，利用成型顆粒圓周表面粗糙形貌所具有的統(tǒng)計(jì)自相似性和標(biāo)度不變特性，采用盒子計(jì)數(shù)法、結(jié)構(gòu)函數(shù)法、變差法3種方法分別計(jì)算出成型顆粒圓周表面的分形維數(shù)D和分形特征參數(shù)G，再根據(jù)W-M分形函數(shù)，建立生物質(zhì)成型顆粒圓周表面粗糙形貌的分形函數(shù)模型，進(jìn)行了數(shù)值模擬。結(jié)果表明：木屑?jí)嚎s成型顆粒圓周表面粗糙度均值為1.45μm時(shí)，D的均值約為1.6，G值約為2.24×10^-5m。分形模型對(duì)木屑?jí)嚎s成型顆粒圓周表面的粗糙形貌模擬準(zhǔn)確合理，所測(cè)得的分形參數(shù)準(zhǔn)確；在測(cè)定分形維數(shù)D的過程中，盒子計(jì)數(shù)法的計(jì)算精度相對(duì)更高。本研究為重構(gòu)準(zhǔn)確可信的生物質(zhì)成型顆粒圓周表面粗糙形貌數(shù)字化模型，實(shí)現(xiàn)成型顆粒圓周表面與成型模具接觸狀態(tài)仿真分析奠定基礎(chǔ)。

　　生物質(zhì)成型顆粒圓周表面粗糙形貌是精確分析生物質(zhì)成型顆粒表面與成型模具之間相互接觸作用的基礎(chǔ)，是分析成型模具所受摩擦磨損機(jī)理并實(shí)現(xiàn)其磨損預(yù)測(cè)的關(guān)鍵。而重構(gòu)準(zhǔn)確、可信的生物質(zhì)成型顆粒圓周表面粗糙形貌數(shù)字化模型，是成型顆粒圓周表面與成型模具接觸模擬仿真，以及成型模具力學(xué)性能、摩擦磨損機(jī)理分析及磨損預(yù)測(cè)的關(guān)鍵[1-2]。

　　分形理論自20世紀(jì)由Mandelbrot創(chuàng)建以來，已廣泛應(yīng)用于分析和處理具有復(fù)雜細(xì)節(jié)特征的自然現(xiàn)象[3-6]。分形理論對(duì)描述具有標(biāo)度率特點(diǎn)的自然現(xiàn)象具有較好適用性[7-10]，此外，生物質(zhì)成型顆粒圓周表面粗糙形貌也具有統(tǒng)計(jì)自相似性和標(biāo)度不變特性[11-14]，因此，可利用分形理論對(duì)生物質(zhì)成型顆粒圓周表面粗糙形貌進(jìn)行分析。

　　近年來，一些學(xué)者[15-20]先后開展了利用分形理論研究金屬接觸表面間的真實(shí)接觸狀況，以解決金屬與金屬接觸面間的摩擦機(jī)理問題，進(jìn)而預(yù)測(cè)摩擦磨損狀況，但目前還鮮見利用分形理論對(duì)生物質(zhì)成型顆粒外表面做的相關(guān)研究，以及對(duì)其與成型孔內(nèi)壁真實(shí)接觸狀況進(jìn)行理論分析。筆者用盒子計(jì)數(shù)法、變差法、結(jié)構(gòu)函數(shù)法3種算法分別計(jì)算出成型顆粒圓周表面分形參數(shù)D和G，并以此為基礎(chǔ)，利用W?M分形函數(shù)，建立起生物質(zhì)成型顆粒圓周表面粗糙形貌分形模型，再通過數(shù)值模擬，實(shí)現(xiàn)其表面形貌重構(gòu)，力求利用W?M分形函數(shù)構(gòu)造出更具普遍意義的生物質(zhì)成型顆粒圓周表面粗糙度曲線。

　　1理論分析及模型建立

　　因環(huán)模成型模孔粗糙表面具有分形特征，基于表面分型參數(shù)接觸模型能夠客觀反映粗糙表面的接觸性質(zhì)，故所建摩擦力公式具有科學(xué)性[11-15]。經(jīng)典接觸力學(xué)指出，當(dāng)固體表面既承受法向載荷又承受切向載荷時(shí):若兩力比值小于0.3，屈服將發(fā)生在表層以下；若兩力比值大于0.3，屈服將發(fā)生在接觸點(diǎn)的邊緣[15-18]。摩擦分子機(jī)械理論指出，在外力作用下，兩摩擦表面間的作用可分為機(jī)械作用和分子作用兩種，即指由于彈塑性變形、微凸體間相互碰撞、嚙合及犁溝效應(yīng)等而阻礙的相對(duì)滑動(dòng)，以及由于分子力作用和分子活動(dòng)使接觸微凸體發(fā)生黏附而產(chǎn)生的滑動(dòng)阻力[17]。表面間分子作用力與機(jī)械阻力之和的切向分量即為摩擦力。

　　2表面輪廓分形維數(shù)計(jì)算方法

　　分形理論作為現(xiàn)代數(shù)學(xué)的一個(gè)分支，可以從分?jǐn)?shù)維度的視角來描述和研究具有自相似性的、不規(guī)則的幾何圖形（如山脈、樹木等）問題[17]。針對(duì)生物質(zhì)成型顆粒圓周表面粗糙形貌的研究，選取計(jì)算分形維數(shù)常用的3種方法———盒子計(jì)數(shù)法、變差法、結(jié)構(gòu)函數(shù)法分別進(jìn)行分形維數(shù)的測(cè)定。

　　3參數(shù)測(cè)定及試驗(yàn)分析

　　3.1試驗(yàn)條件

　　試驗(yàn)用成型顆粒樣本由木屑（呼和浩特市周邊的松樹和楊樹混合木屑）經(jīng)生物質(zhì)成型機(jī)壓縮制成，其顆粒度為1~3mm、含水率約11%、密度約1.2g/cm³。樣本制作工藝流程:生物質(zhì)環(huán)模成型機(jī)由電機(jī)（功率7.5kW）帶動(dòng)環(huán)模旋轉(zhuǎn)，物料與環(huán)模間摩擦力和物料與壓輥間摩擦力使壓輥?zhàn)赞D(zhuǎn)，物料在環(huán)模與壓輥間形成的楔形空間受擠壓力作用而被擠入環(huán)模成型孔（成型模孔長徑比5∶1）內(nèi)，并逐漸從環(huán)模孔以柱狀形式被擠出。

　　主要測(cè)試儀器:JB?8C型精密粗糙度儀（廣精精密儀器有限公司）；DHS?10A型快速水分測(cè)定儀；100mL量筒（精度1mL）；網(wǎng)孔直徑3mm的標(biāo)準(zhǔn)檢驗(yàn)篩（符合GB/T6003.1—1997《金屬絲編織網(wǎng)試驗(yàn)篩》要求）；JAEIHAENE型電子秤（精度0.01g）；游標(biāo)卡尺；秒表（精度0.01s）。

　　3.2試驗(yàn)方法

　　將生物質(zhì)環(huán)模成型機(jī)生產(chǎn)的直徑為6mm的木屑?jí)嚎s成型顆粒，進(jìn)行密度和含水率的測(cè)量，然后利用粗糙度儀對(duì)成型顆粒圓周表面粗糙形貌進(jìn)行測(cè)量并提取數(shù)據(jù)，再利用3種分形維數(shù)方法計(jì)算成型顆粒圓周表面粗糙形貌的分形維數(shù)D。

　　3.2.1成型顆粒密度計(jì)算

　　取若干成型顆粒，將其端面磨平后采用游標(biāo)卡尺測(cè)出顆粒長度與直徑，并稱得質(zhì)量，最后求得顆粒密度。

　　3.2.2表面粗糙形貌測(cè)量

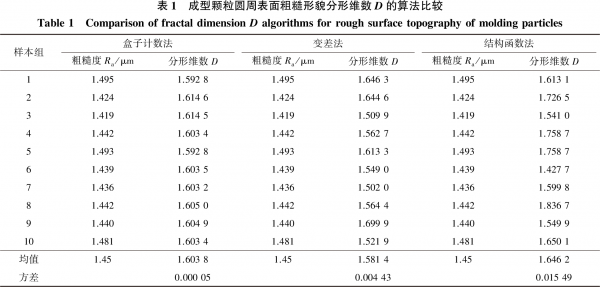
　　選出直徑為6mm的10組（每組10個(gè)成型顆粒樣本）木屑?jí)嚎s成型顆粒樣本，利用粗糙度儀對(duì)每一顆粒樣本的圓周表面粗糙狀態(tài)進(jìn)行軸向形貌測(cè)量，獲得表面輪廓曲線，提取其表面輪廓曲線數(shù)據(jù)后，再利用3種分維算法計(jì)算生物質(zhì)成型顆粒圓周表面粗糙形貌分形維數(shù)D值。

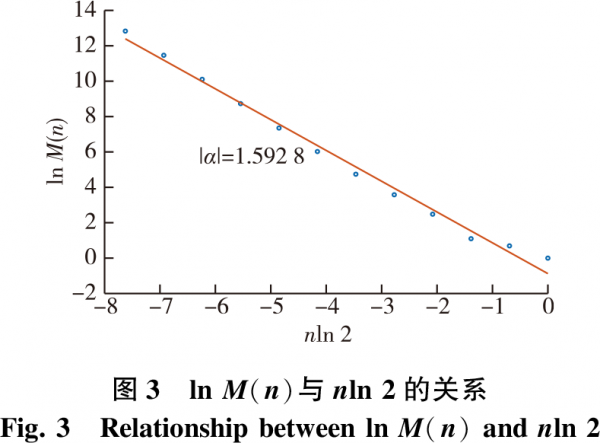
　　1）盒子計(jì)數(shù)法。根據(jù)盒子計(jì)數(shù)法計(jì)算分維的原理，實(shí)現(xiàn)不同大小的網(wǎng)格（設(shè)n=1，2，…，11）對(duì)所測(cè)樣本粗糙表面輪廓進(jìn)行動(dòng)態(tài)覆蓋，再利用MATLAB對(duì)網(wǎng)格邊長2-n和網(wǎng)格數(shù)目2n分別進(jìn)行統(tǒng)計(jì)，再采用最小二乘法對(duì)二者進(jìn)行對(duì)數(shù)擬合，所擬合出的圖形斜率α（圖3）絕對(duì)值即為分形維數(shù)D值，計(jì)算結(jié)果如表1所示。

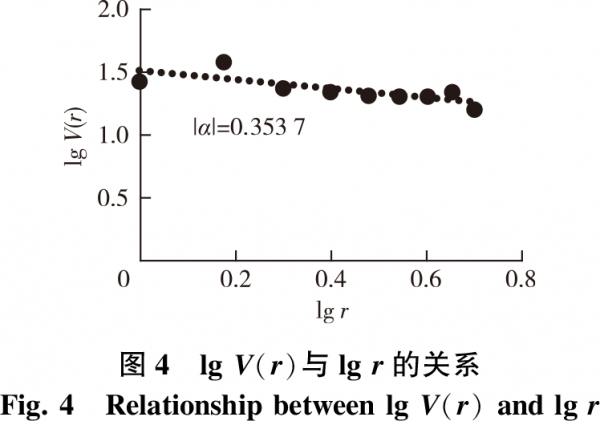
　　2）變差法。對(duì)所測(cè)樣本粗糙表面輪廓形貌，分別取尺度r為1，2，…，10μm，測(cè)出對(duì)應(yīng)的Hi值，利用式（8）計(jì)算出對(duì)應(yīng)的V（r）值，建立lgV（r）與lgr為坐標(biāo)軸的散點(diǎn)圖，進(jìn)行數(shù)據(jù)擬合后得出直線，求出斜率α（圖4），將其絕對(duì)值代入式（9），求得分形維數(shù)D值，計(jì)算結(jié)果如表1所示。

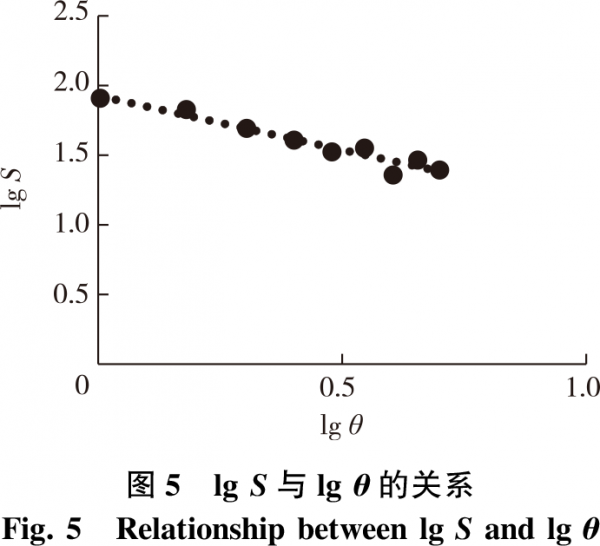
　　3）結(jié)構(gòu)函數(shù)法。對(duì)所測(cè)樣本粗糙表面輪廓形貌，分別取θ為1，2，…，10μm，測(cè)出對(duì)應(yīng)的表面粗糙高度z（x+θ）及z（x）值，并利用式（10）計(jì)算出對(duì)應(yīng)的S（θ）值，建立lgS與lgθ為坐標(biāo)軸的散點(diǎn)圖，進(jìn)行數(shù)據(jù)擬合后得出直線，求出斜率α（圖5），將其絕對(duì)值代入式（11），求得分形維數(shù)D值，計(jì)算結(jié)果如表1所示。

　　3.3試驗(yàn)結(jié)果與分析

　　所取樣本經(jīng)過3種分維算法后得到的生物質(zhì)成型顆粒圓周表面粗糙形貌分形維數(shù)D值見表1。由表1可知，生物質(zhì)成型顆粒圓周表面的粗糙度均值為1.45μm時(shí)，粗糙形貌分形維數(shù)D的均值約為1.6（保留一位小數(shù)后）。樣本表面輪廓采樣長度L取50μm，其輪廓的分辨率δ取0.001，并與分形維數(shù)D一起代入式（6）后計(jì)算得出分形特征參數(shù)G=2.24×10^-5m。

　　由表1分析可知，盒子計(jì)數(shù)法、變差法及結(jié)構(gòu)函數(shù)法3種算法所測(cè)出的分形維數(shù)D相同，均約為1.6，但略有區(qū)別。結(jié)構(gòu)函數(shù)算法計(jì)算D所得數(shù)據(jù)最大，D的均值達(dá)到1.6462，方差也最高，達(dá)到0.01549；變差算法計(jì)算D所得數(shù)據(jù)最小，D的均值為1.5814，方差達(dá)0.00443；盒子計(jì)數(shù)法計(jì)算D所得數(shù)據(jù)居中，D的均值為1.6038，方差最小，僅為0.00005。因此，經(jīng)分析得出，由于盒子計(jì)數(shù)法計(jì)算所得樣本方差相對(duì)最小，用環(huán)模生物質(zhì)成型機(jī)生產(chǎn)的密度為1.2g/cm³的生物質(zhì)成型顆粒圓周表面粗糙形貌的分形維數(shù)D測(cè)量中，采用盒子計(jì)數(shù)法計(jì)算分形維數(shù)D值相對(duì)精度更高。

　　4成型顆粒表面粗糙形貌模擬

　　4.1二維仿真模擬

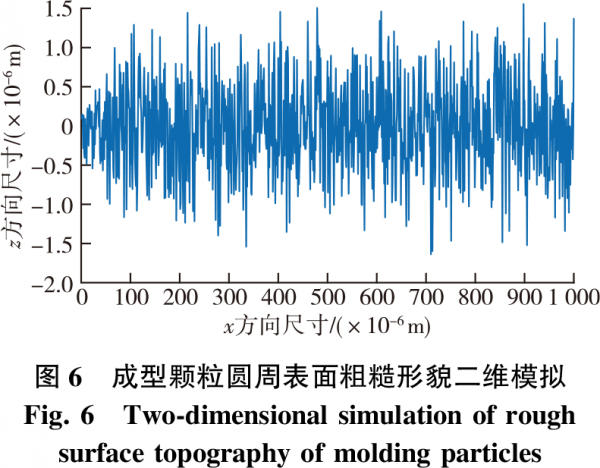
　　將上述計(jì)算結(jié)果代入式（6）后，編寫二維隨機(jī)粗糙表面程序，利用MATLAB進(jìn)行模擬計(jì)算，對(duì)成型顆粒圓周表面粗糙形貌進(jìn)行數(shù)值模擬。具體參數(shù)設(shè)置:分形維數(shù)D=1.6，分形特征參數(shù)G=2.24×10-5m，輪廓分辨率δ=0.001，輪廓采樣長度L=50μm。模擬后的結(jié)果如圖6所示。

　　4.2三維仿真模擬

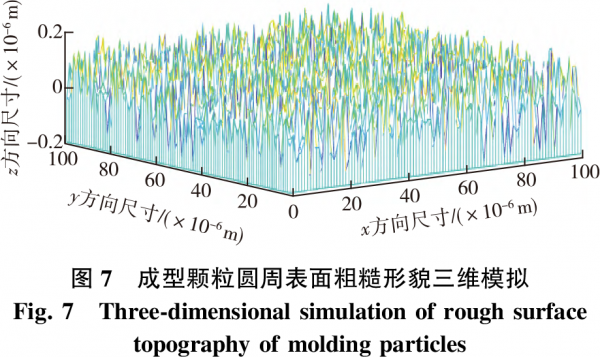
　　根據(jù)上述計(jì)算結(jié)果，對(duì)成型顆粒粗糙表面輪廓，利用式（6）在MATLAB中進(jìn)行計(jì)算后再經(jīng)過三維空間隨機(jī)轉(zhuǎn)化計(jì)算，得到的三維形貌視圖結(jié)果如圖7所示。

　　4.3模擬試驗(yàn)結(jié)果分析

　　將實(shí)測(cè)木屑成型顆粒粗糙表面所得分形參數(shù)D、G作為數(shù)據(jù)仿真的初始值，利用W?M分形函數(shù)對(duì)其輪廓形貌進(jìn)行模擬，結(jié)果如圖6（二維視圖）和圖7（利用MATLAB進(jìn)行隨機(jī)轉(zhuǎn)化得到三維視圖）所示。成型顆粒圓周表面粗糙形貌電鏡放大100倍下的掃描狀態(tài)見圖8，其中暗色區(qū)表示顆粒表面比較光滑，白色線條區(qū)表示非光滑表面，白色線條越多表明成型顆粒圓周表面孔隙越多、密度越低，也越粗糙。

　　為了對(duì)模擬結(jié)果進(jìn)行分析，需要對(duì)圖3中的模擬粗糙形貌數(shù)據(jù)進(jìn)行采集后與圖8的表面粗糙形貌作對(duì)比分析。針對(duì)木屑?jí)嚎s成型顆粒表面粗糙形貌的輪廓算數(shù)平均偏差Ra、平均輪廓波峰高度Rp、輪廓單元平均寬度Rsm、粗糙度峰值數(shù)Rpc、輪廓支承比率Rmr這5個(gè)重要參數(shù)進(jìn)行對(duì)比探討。圖3中，模擬輪廓算數(shù)平均偏差Ra=1.432μm（實(shí)測(cè)Ra=1.495μm），模擬平均輪廓波峰高度Rp=2.84μm（實(shí)測(cè)Rp=2.776μm），模擬輪廓單元平均寬度Rsm=0.178mm（實(shí)測(cè)Rsm=0.182mm，如圖8所示），模擬粗糙度峰值數(shù)Rpc=30峰/mm（實(shí)測(cè)Rpc=32.5峰/mm），模擬輪廓支承比率Rmr=89.8%（實(shí)測(cè)Rmr=93.6%）。

　　根據(jù)上述數(shù)據(jù)分析結(jié)果，模擬參數(shù)Ra、Rp、Rsm、Rpc、Rmr與實(shí)測(cè)參數(shù)接近程度（模擬值/實(shí)測(cè)值）分別為95.8%，102.3%，97.8%，92.3%，95.9%，說明利用W?M分形函數(shù)模擬木屑?jí)嚎s成型顆粒數(shù)據(jù)基本準(zhǔn)確合理。由此可知，所測(cè)得的分形維數(shù)D及分形特征參數(shù)G正確，所用粗糙表面分形模擬模型對(duì)生物質(zhì)成型顆粒圓周表面粗糙形貌的模擬是合理的。

　　5結(jié)論

　　對(duì)于以混合木屑為原料、顆粒度1~3mm、含水率11%、直徑6mm、密度1.2g/cm³的生物質(zhì)成型顆粒，采集其圓周表面粗糙形貌數(shù)據(jù)，采用盒子計(jì)數(shù)法、結(jié)構(gòu)函數(shù)法、變差法3種方法分別計(jì)算出粗糙表面分形模型的關(guān)鍵參數(shù)（分形維數(shù)D和分形特征參數(shù)G），再根據(jù)W?M分形函數(shù)，建立了生物質(zhì)成型顆粒圓周表面粗糙形貌分形模型，并進(jìn)行數(shù)值模擬，得到如下主要結(jié)論。

　　1）生物質(zhì)成型顆粒圓周表面的粗糙度均值為1.45μm時(shí)，粗糙形貌分形維數(shù)D的均值約為1.6，分形特征參數(shù)G約為2.24×10^-5m。

　　2）模擬結(jié)果表明，粗糙表面分形模擬模型對(duì)生物質(zhì)成型顆粒圓周表面的粗糙形貌模擬準(zhǔn)確合理，所測(cè)得的分形維數(shù)D及分形特征參數(shù)G準(zhǔn)確，所用粗糙表面分形模型對(duì)生物質(zhì)成型顆粒圓周表面粗糙形貌的模擬是合理的，且具有普遍意義。

　　3）采用盒子計(jì)數(shù)法、變差法及結(jié)構(gòu)函數(shù)法3種方法測(cè)定生物質(zhì)成型顆粒圓周表面粗糙形貌分形維數(shù)D的過程中，盒子計(jì)數(shù)法的計(jì)算結(jié)果最可信，計(jì)算精度相對(duì)更高。